天龙八部归来：助边数据已被博士生玩家破解？龙妹直呼涨知识！

开始吐槽

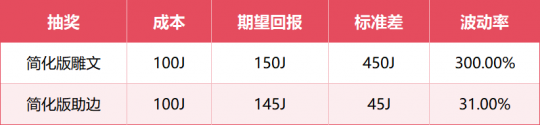
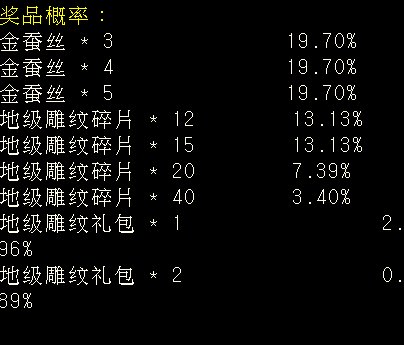
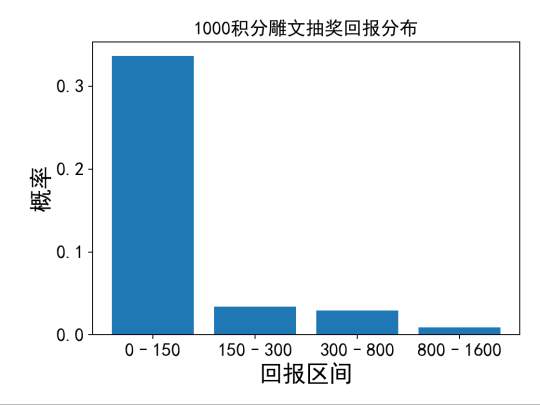
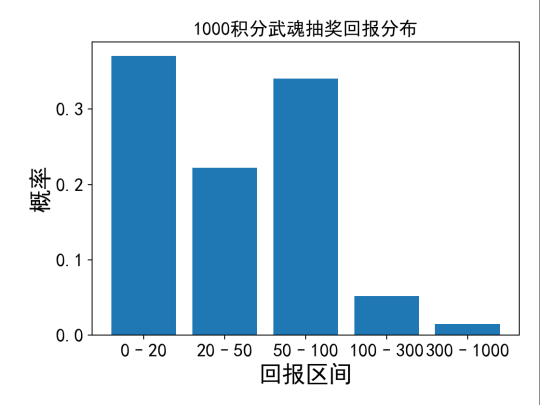
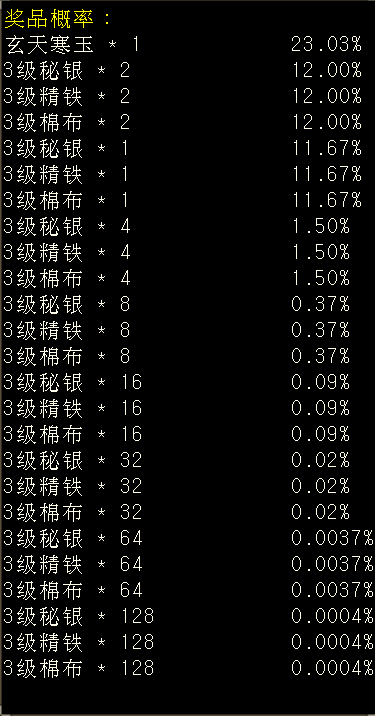
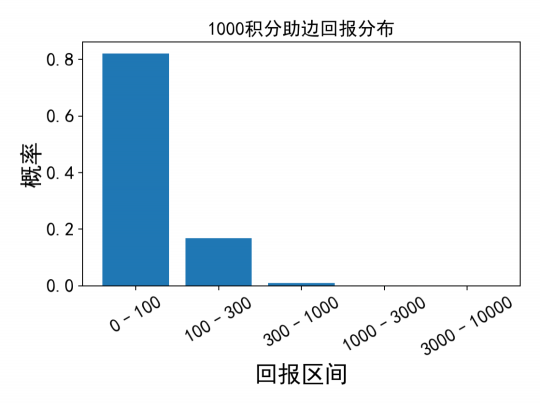
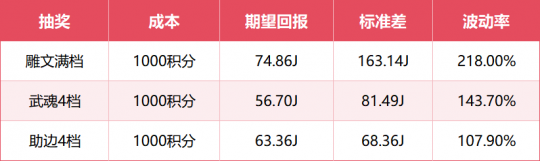
　　一、简介

　　抽奖是天龙归来的核心玩法之一，雕文、武魂、助边更是大家每周一必参加的活动。很多玩家因此一夜暴富，满6带5，也有玩家血本无归。

　　在这篇攻略之前，已经有不少主播发布了许多关于抽奖的攻略，主要是公布了各个材料的贡献分数、各个档位和次数所需的分数等。基于这些信息，大部分玩家都可以选择购买最经济的材料，参与某一档位的抽奖。

　　因此，本文想给大家带来一些更为深入的分析：给定一定的分数（如1000分，即200元宝价值的物品），我们应该选择参与哪一个赌桌？每个赌桌的期望回报是多少，每次收益的分布又如何？相比传统只看“期望”的攻略，本文想给大家带来一些更深入的视角，即波动控制。

　　为何要研究波动？这里有个很简单的例子，如果有2个游戏，第一个游戏你有10%的概率获得100元，90%概率获得0元。第二个游戏你有100%的概率获得10元？你会玩哪个？

　　我相信大部分人在这种情况下都会选择第二个游戏。因为第一个游戏的期望回报也是100*0.1=10元，但是你却要承担很多时候血本无归的风险。这就是行为学中的“风险厌恶”。

　　更极端一些，就算第二个游戏是100%概率获得9元，我相信还是有很多人会选择第二个游戏，来规避风险和波动。这和股票市场也很相似，大部分人宁可选择稳定、回撤小，年化收益更低的货币基金，也不愿选择收益更高，但是风险也更大的股票投资。

　　因此，在这篇攻略里，我们会深入研究各个抽奖玩法的期望奖励与其对应的波动，看看是否存在“收益又高，风险又低”的抽奖项目，帮助大家用科学对抗玄学

　　二、核心方法

　　在讲解结果之前，我们先讲一下核心的方法（对数学不感兴趣的可以直接跳过）。对于每一次抽奖，我们都可能有不同的收益，如果用X来表示这个结果的随机变量，那么我们首先可以计算这个随机变量的期望E(X)，以及标准差Std(X)，大家常常用Std(X)除以E(X)来表示波动的大小。同时，我们会用P(X)表示这个随机变量的分布，不同的分布带来的波动结果也不一样。

　　一个简单的例子：假设大家在玩一个简化版的雕文抽奖（成本100J），满档1次，只有金蚕丝和雕文礼包2种奖励，金蚕丝概率90%（假设价值0金），礼包概率10%（假设价值1500金）。那么我们的X会有2种取值：1）X=0，2）X=1500金。那么这次抽奖回报的期望就是：

　　E(X) = 0 * 0.9 + 1500 * 0. 1 = 150J

　　假设现在还有一个简化版本的助边（成本也是100J），满档1次，只有1个精铁（价值90金）和1个秘银（价值200金）2种奖励，概率都为0.5，那么抽助边的期望回报就是：

　　E(X) = 90 * 0.5 + 200 * 0. 5 = 145J

　　如果只从期望上来看，似乎雕文抽奖更划算一些。实际上大家还应该考虑波动。对于雕文而言，其收益的标准差为：Std(X) =450J （具体计算方法我就省略了） , 而助边收益的标准差为：Std(X) =55J。标准差的物理理解，大家可以简单理解为，每次抽奖，收益在均值上下波动的大小。也就是说，对于助边而言，虽然每次平均回报只有145J，但是大部分时候我是在145上下45J波动，也就是100J ~ 190J 范围内波动的，也就是大家常说的，“亏也亏不到哪去”。但是对于雕文而言，波动却高达450J。这种时候，大家还会选择抽雕文吗？愿意承受很多时候就一个金蚕丝的波动，来换取额外5J的期望回报吗？相信很多人答案是否定的。

　　总结一下上面的例子，我们在都是100J的成本的情况下，如果考虑波动率，其实简化版的助边更合适，可以帮助我们控制回撤，稳住心态，长期的玩下去。

　　所以，接下来我们就来看看游戏中实际的雕文、武魂、助边的期望回报和波动

　　三、雕文、武魂、助边

　　首先我们得分析和结论基于以下假设：系统里给的奖励概率都是准确的。物价基于当前天龙一区的物价。这里我们选取3个最有代表性的例子：

　　地级雕文，满档3-4次（实际3次），需要6500分，平均每次需要2166.7分

　　助边4档，需要13000分（助边4档既可能出4次奖励，也可能出5次奖励，具体概率未知，这里假设为4.5次，由于4-5次产生的波动在这里忽略不计），平均每次需要2888.9分

　　武魂4档，2-3次（实际2次），需要8200分），平均每次需要4100分

　　注意：下面的分析都是采用1次抽奖对应的成本 + 波动率。次数本质上是有玩家自己可以控制的，次数越多，波动越小，所以我们对所有抽奖的分析都不考虑次数的影响。

　　3.1 地雕分析

　　首先附上地雕满档的概率描述：

　　我们做一些保守的假设，金蚕丝一文不值。雕文礼包价值 = 100个碎片，单个碎片价值16J，那么我们可以得出，每次游戏（税后）：

　　期望回报：E(X) = 161.95J

　　标准差：Std(X) = 336.26J

　　波动率：336.26J / 161.95J = 207%

　　一次抽奖的成本是6500 / 3 = 2166.7分。为了统一后续所有的分析，我们将所有的数值都转化成1000积分对应的数值，也就是成本为1000分的情况，需要把所有数值都乘以(1000/2166.7)：

　　同时，我们可以可视化一下每次游戏（转换到1000积分情况下）的收益的分布P(X):

　　3.2 武魂分析

　　首先附上武魂4档的概率描述：

　　假设单个碎片价值12J，回天神石65J，破天箭21J，那么我们可以得出，每次游戏（税后）：

　　期望回报：E(X) = 232.63J

　　标准差：Std(X) = 334.31J

　　波动率：334.31J ?/ 232.63J = 143.7%

　　一次抽奖的成本是8200 / 2 = 4100分。我们将所有的数值都转化成1000积分对应的数值，需要把所有数值都乘以(1000/4100)：

　　同时，我们可以可视化一下每次游戏（转换到1000积分情况下）的收益的分布P(X):

　　3.3 助边分析

　　首先附上助边4档的概率描述：

　　假设寒玉154J，3级秘银197J，3级精铁90J，3级精铁棉布120J，那么我们可以得出，每次游戏（税后）：

　　期望回报：E(X) = 206.34J

　　标准差：Std(X) = 222.62J

　　波动率：334.31J ?/ 232.63J = 107.9%

　　一次抽奖的成本是13000 / 4.5 = 2888.9分。我们将所有的数值都转化成1000积分对应的数值，需要把所有数值都乘以(1000/2889)：

　　同样，对分布做一个可视化：

　　四、总结

　　将上述3个结果总结，在统一到1000积分成本的情况下：

　　雕文的期望回报最高，同时波动也最大，而助边的期望回报第二高，波动率最小，大概率不会亏很多。武魂是这里面性价比最低的，不仅期望回报最低，波动也比助边大。因此，在目前的物价情况下，我推荐：

　　金币很多的玩家，地雕文拉满，通过增加次数，减少波动，如果1000积分的成本低于74J，长期来看是会赚钱的，更何况金蚕丝还能给一些补充。

　　助边虽然波动低，但是从目前的物价来看期望回报和地雕文差的有点多，等待精铁、秘银、玄天寒玉涨价后（存在一定可能），如果期望回报和雕文类似的，应该全部all-in 助边，达到回报与风险控制双收。

　　武魂别碰（除非回天神石、破天箭价格大涨，但是基本不太可能，这两个材料产出太多，消耗太少）

　　最后想说一下，如果大家观察所有抽奖的回报分布，基本都是一个右偏长尾的分布，大部分的概率都落在前面收益较低的部分。也就是说，抽奖的大部分的体验就是：大部分时候一直小亏，突然一波猛赚，收回所有之前的亏损还有盈余。所以，在成本小于期望回报的情况下，请大家坚持抽奖，相信概率与统计的力量，阳光总在风雨后，祝大家游戏愉快。

　　>>>轻松天龙即刻开打！点击下载《天龙八部·归来》

>>>进群有福利，速度加入【天龙八部·归来玩家交流群1】：785864921（←点击加入我们）。